发表自话题：第七次人口普查数据结构
前言
《数据结构》和《算法导论》应该是程序猿的必修课吧 ️？？？
之前在学习《数据结构》的时候，零零散散写了一些笔记，最近把它们总结了一下。算是阶段性的学习成果吧～
《数据结构（C++版）邓俊辉 第三版》《数据结构（C++版）习题解析 第三版 邓俊辉》邓俊辉《数据结构》视频（PS：以上三份资料可以私聊我获取，因为我上次发了一个matlab的安装链接被知乎告知违规了 ！！！！）
算法
定义：特定的计算模型下， 旨在解决特定问题的指令序列输入：待处理的信息（问题）输出：经处理的信息（答案）正确性：的确可以解决指定的问题确定性：任一算法都可以描述为一个由基本操作组成的序列可行性：每一基本操作都可实现，且在常数时间内完成有穷性：对于任何输入，经有穷次基本操作，都可以得到输出时间复杂度
特定算法处理规模为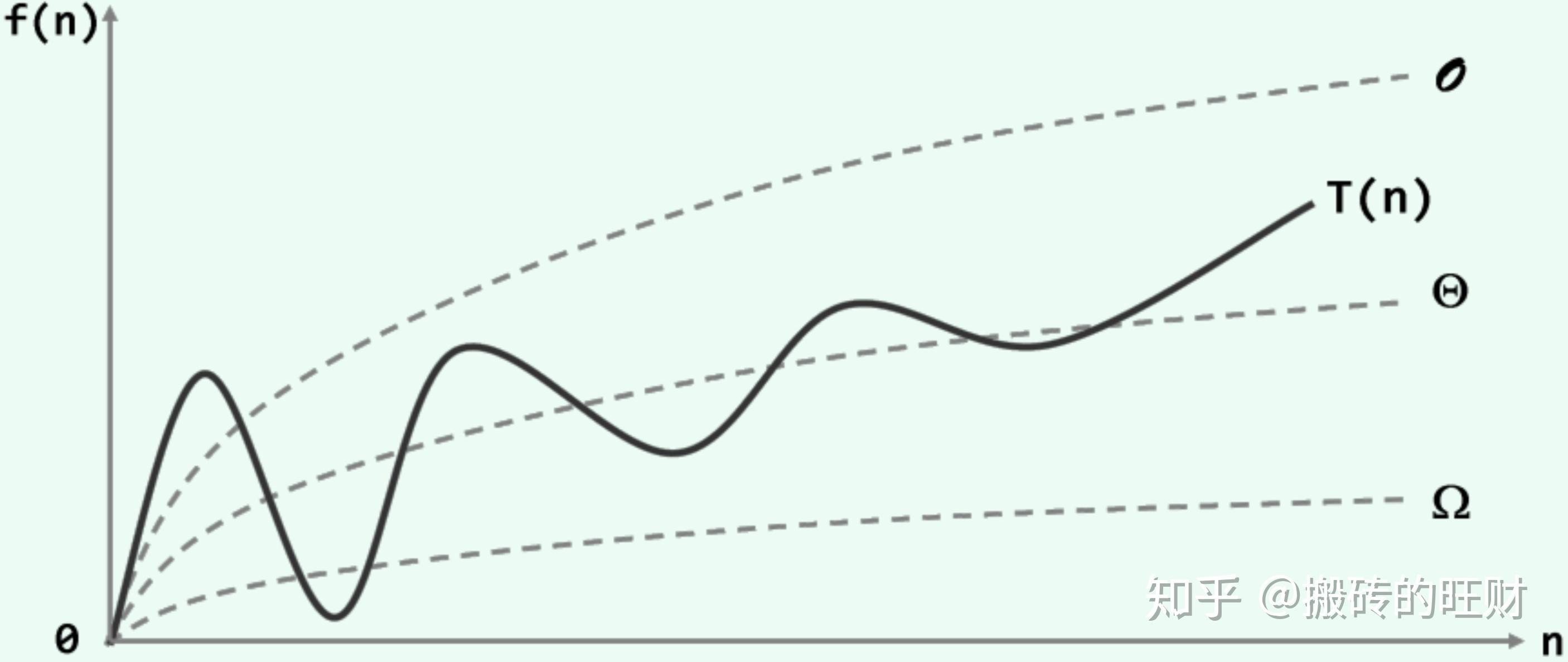 
复杂度分析常数 
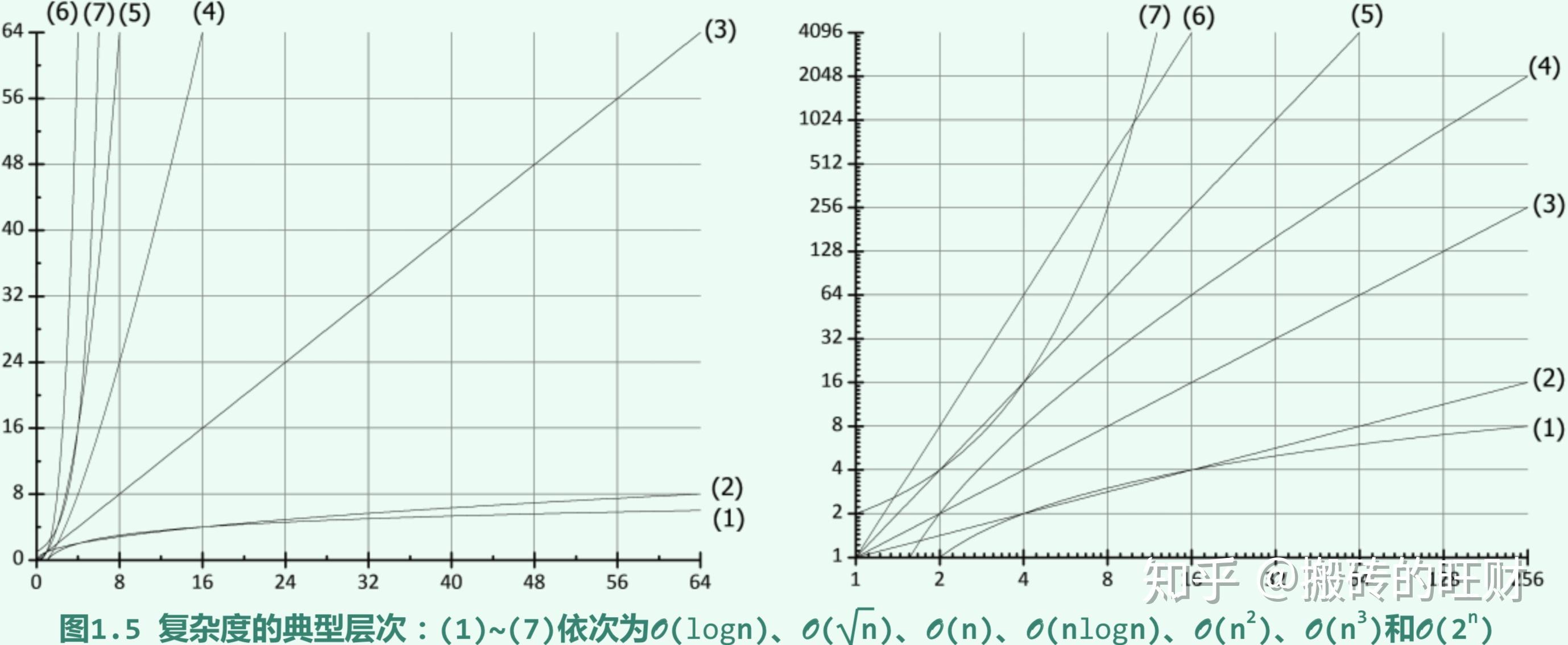级数
1. 算数级数：与末项平方同阶
算数级数： 
2.
算数级数：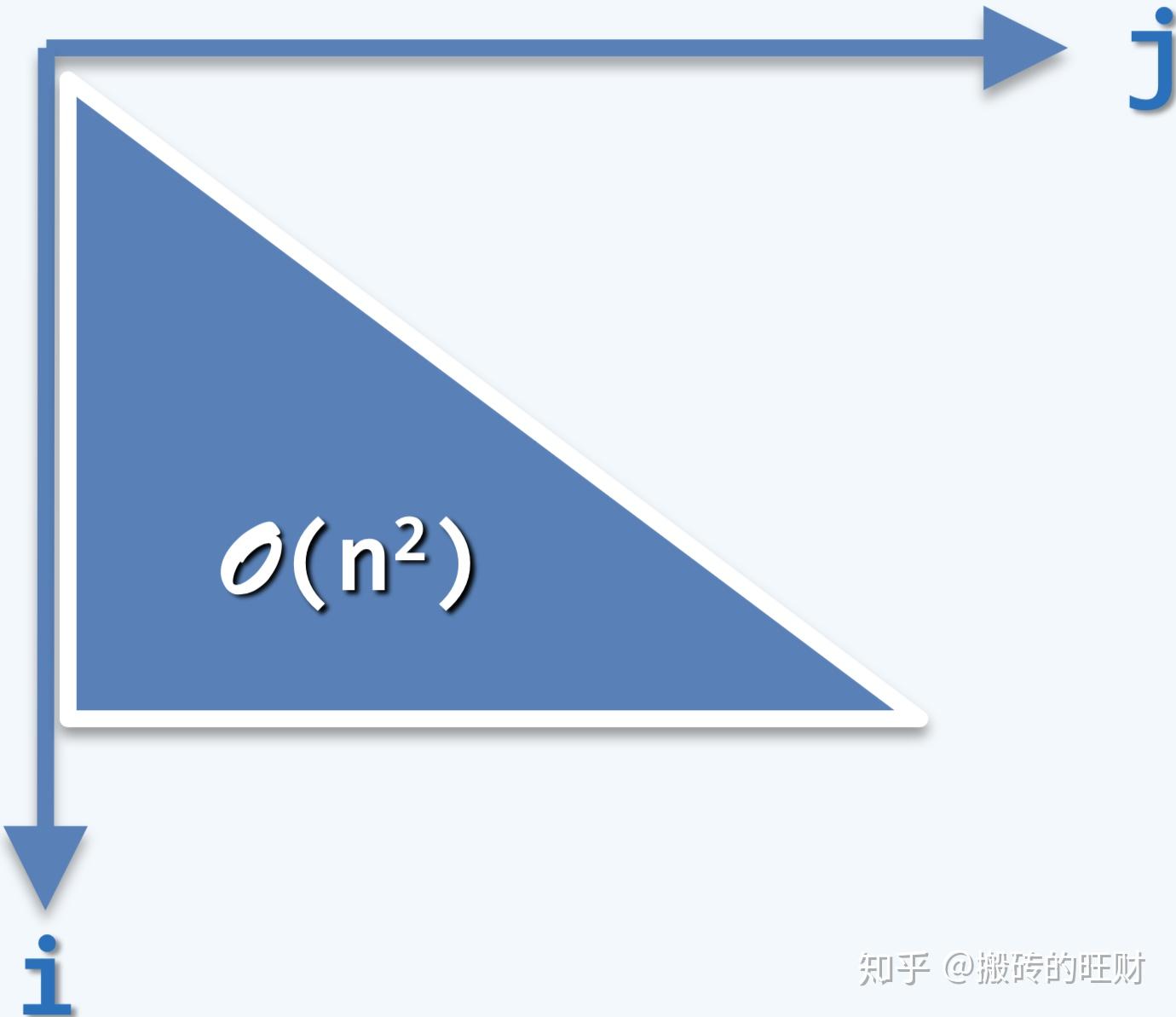 
3.
算数级数
4.
（注：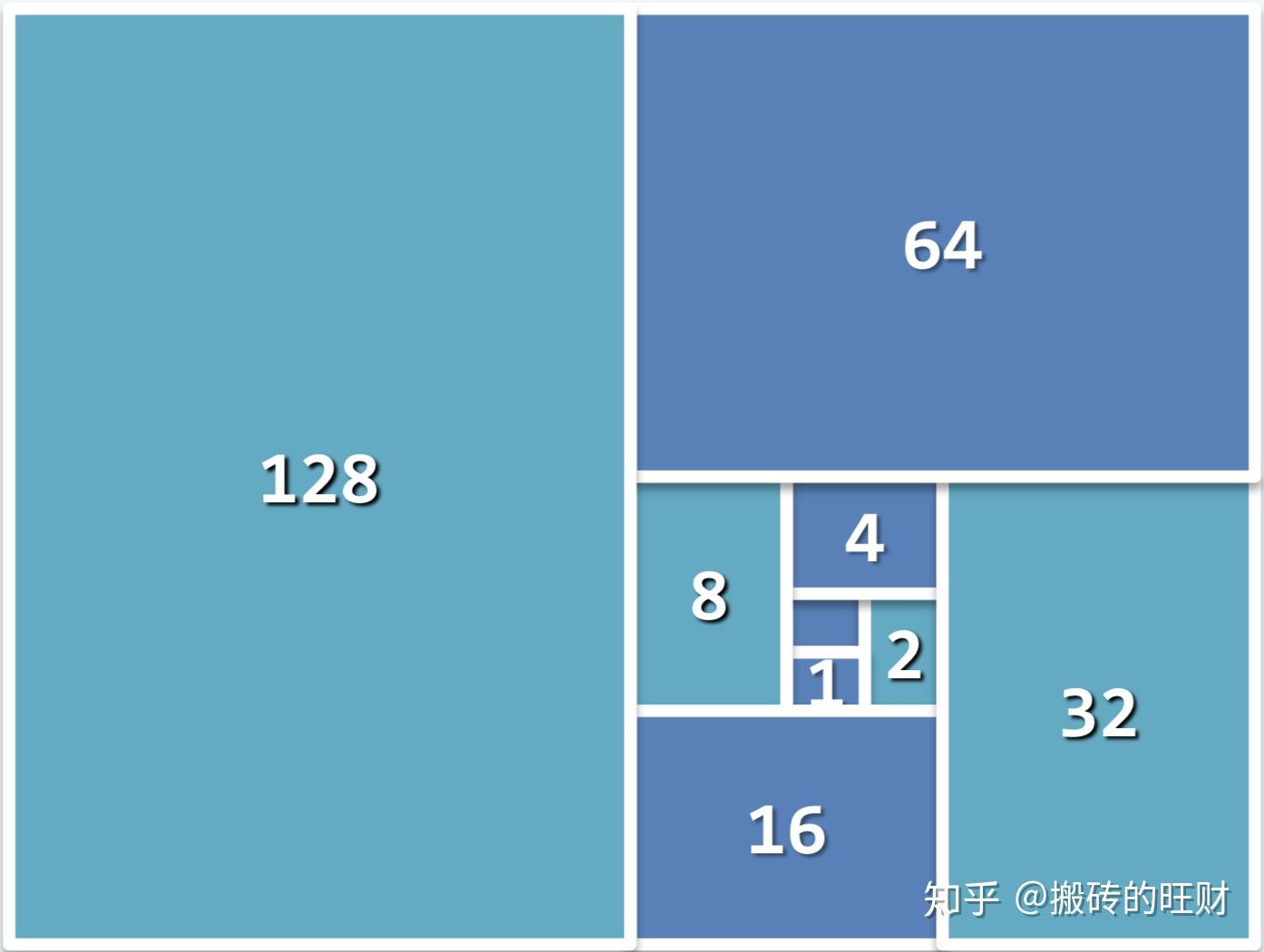 
5.
几何级数： 
起泡排序
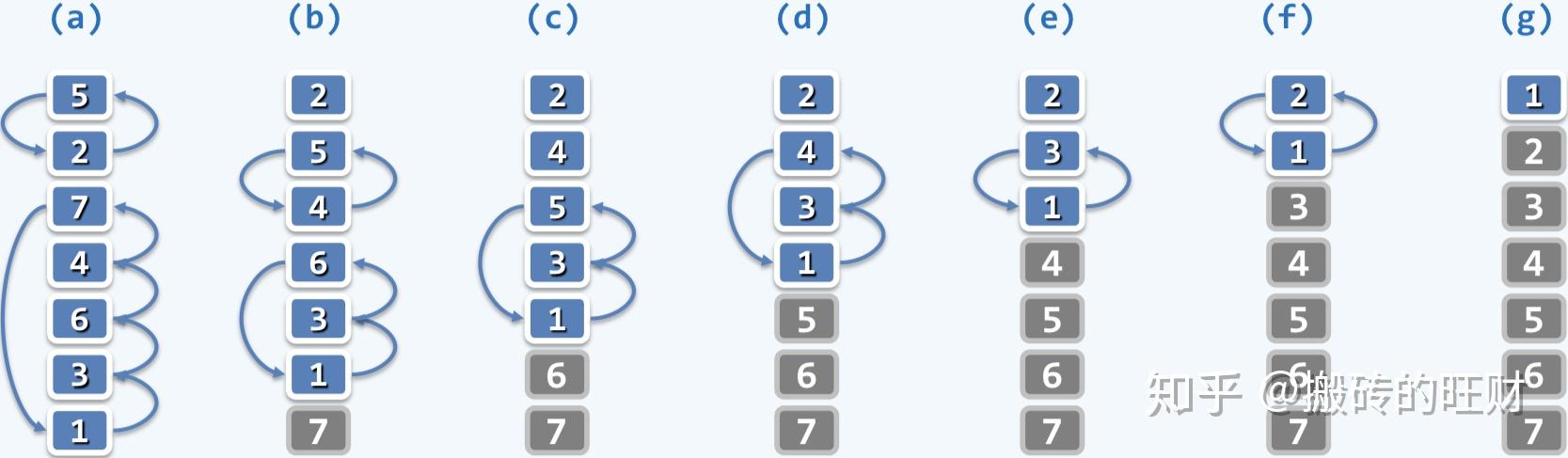最坏情况：输入数据反向排列此时共需 
减而治之（decrease and conquer）
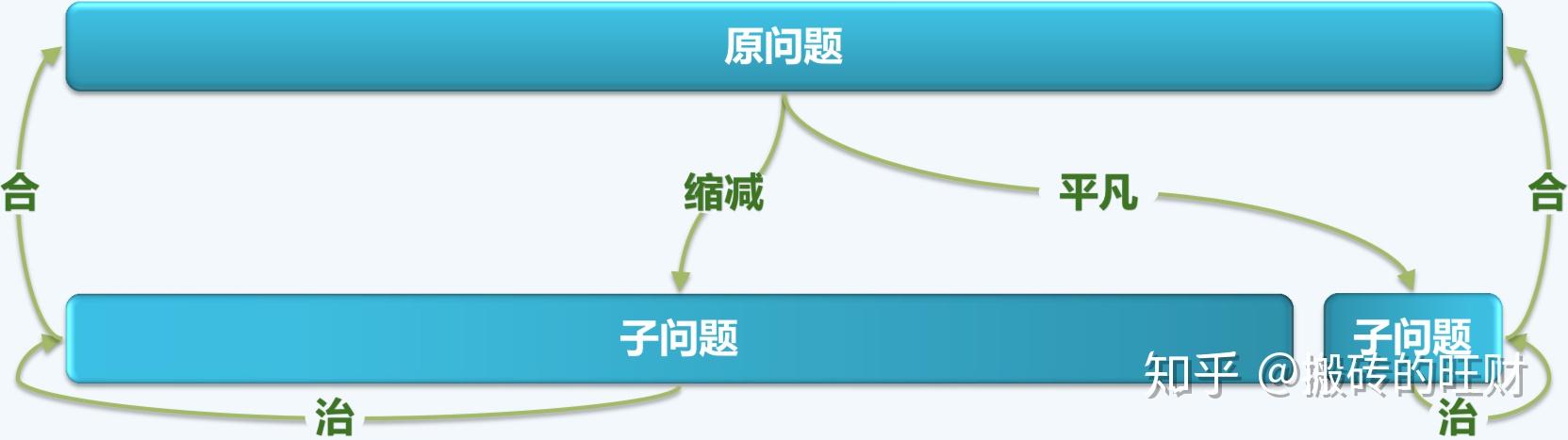
为求解一个大规模的问题，可以将其划分为两个子问题：其一平凡，另一规模缩减。分别求解子问题，由子问题的解，得到原问题的解。
数组求和：迭代问题：计算任意
（注：计算时间复杂度时，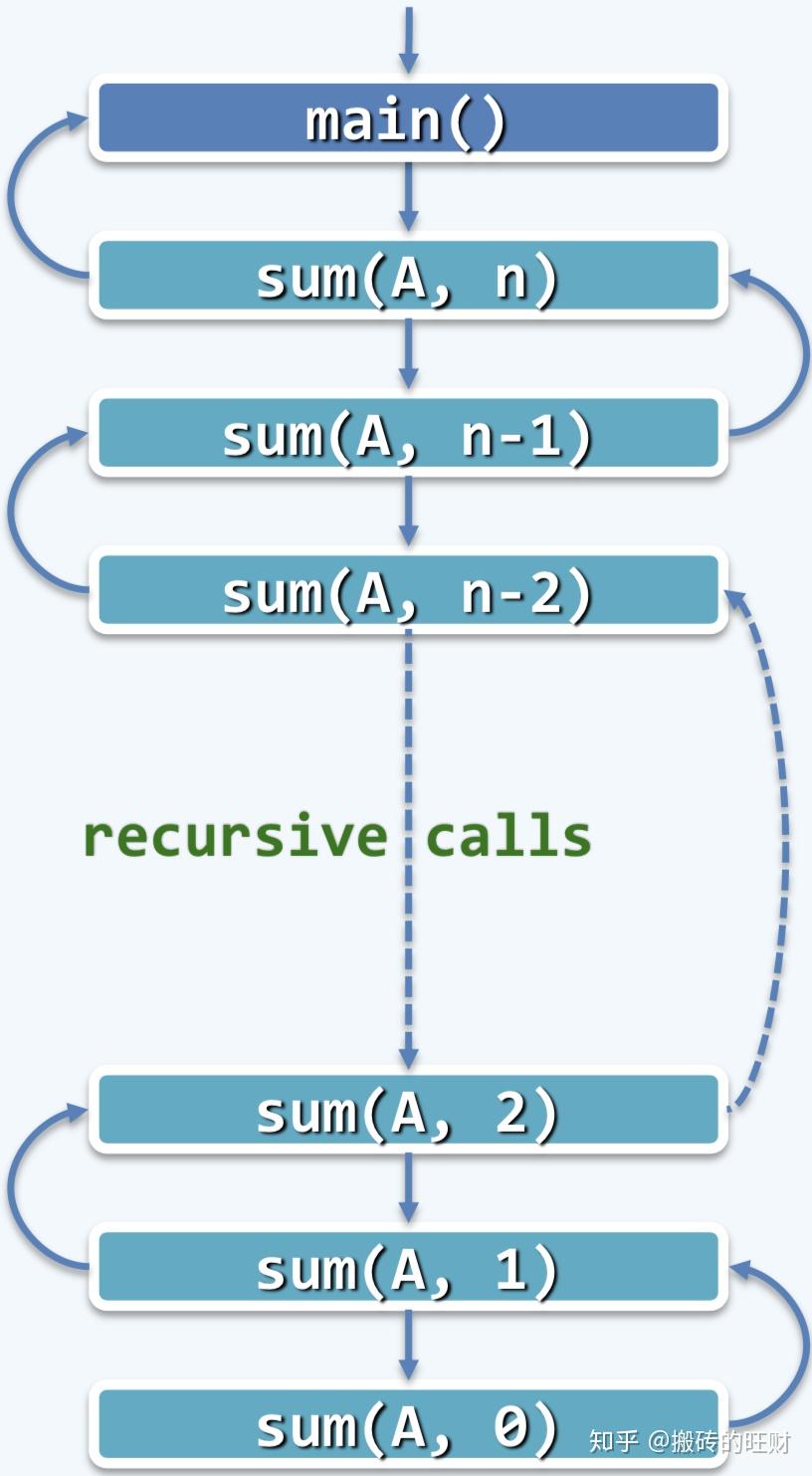 
从递推的角度看，为求解 
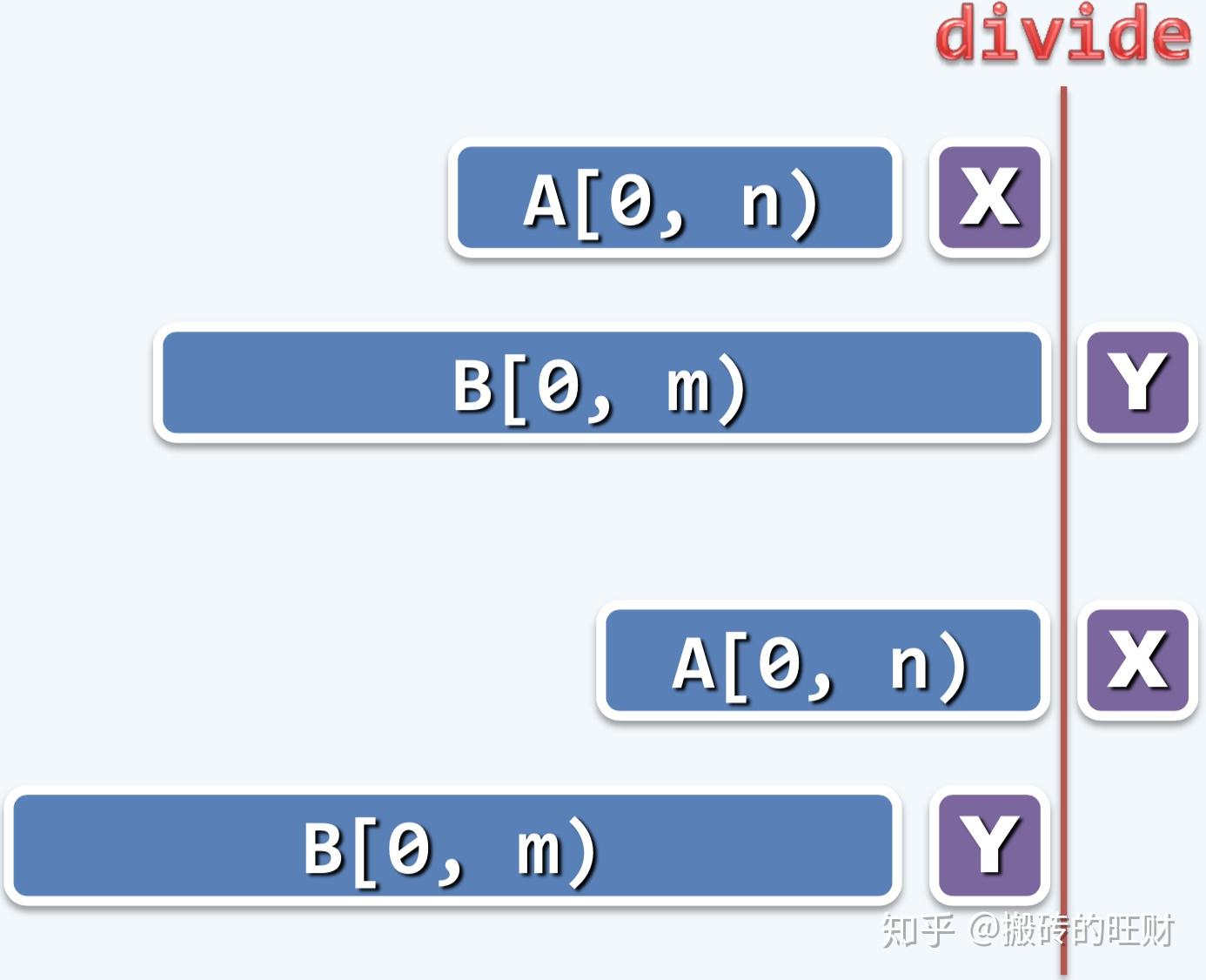
为求解一个大规模的问题，可以将其划分为若干（通常两个）子问题，规模大体相当。分别求解子问题，由子问题的解，得到原问题的解。
数组求和：二分递归
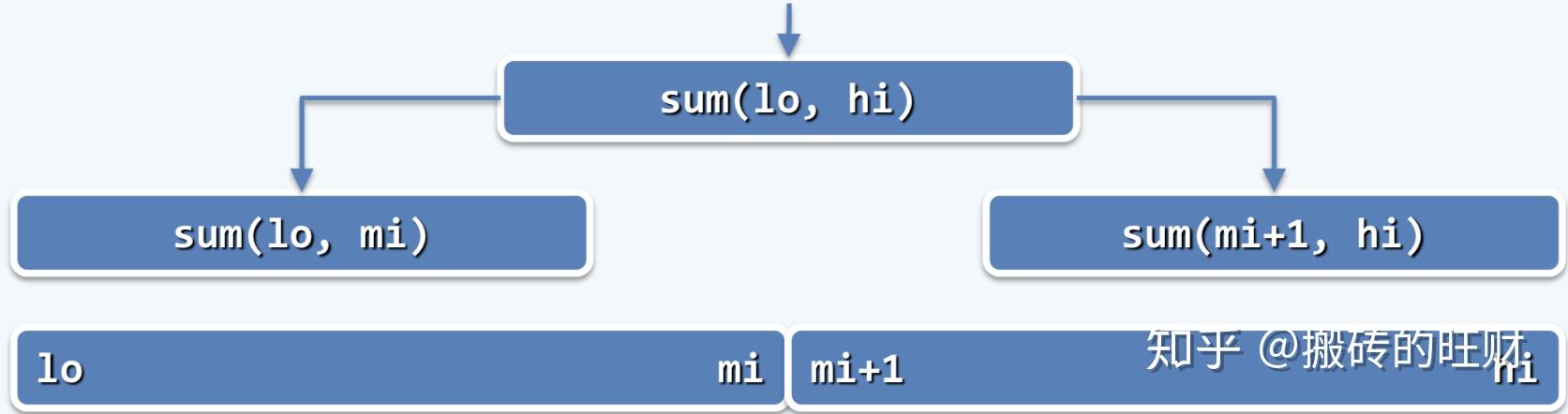
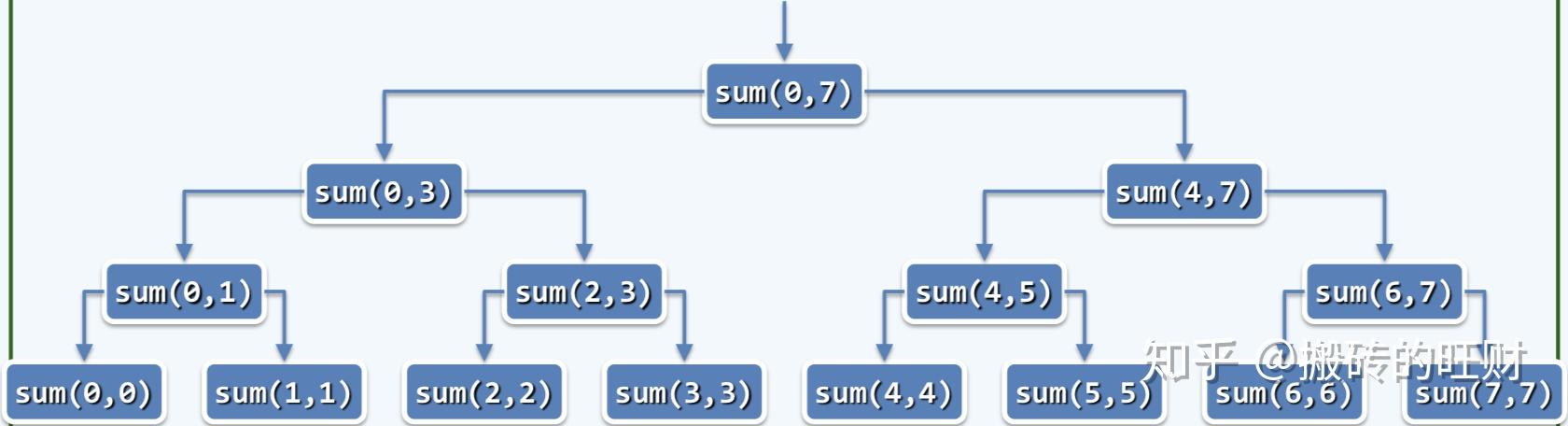
运用递归跟踪：
动态规划
fib()：递归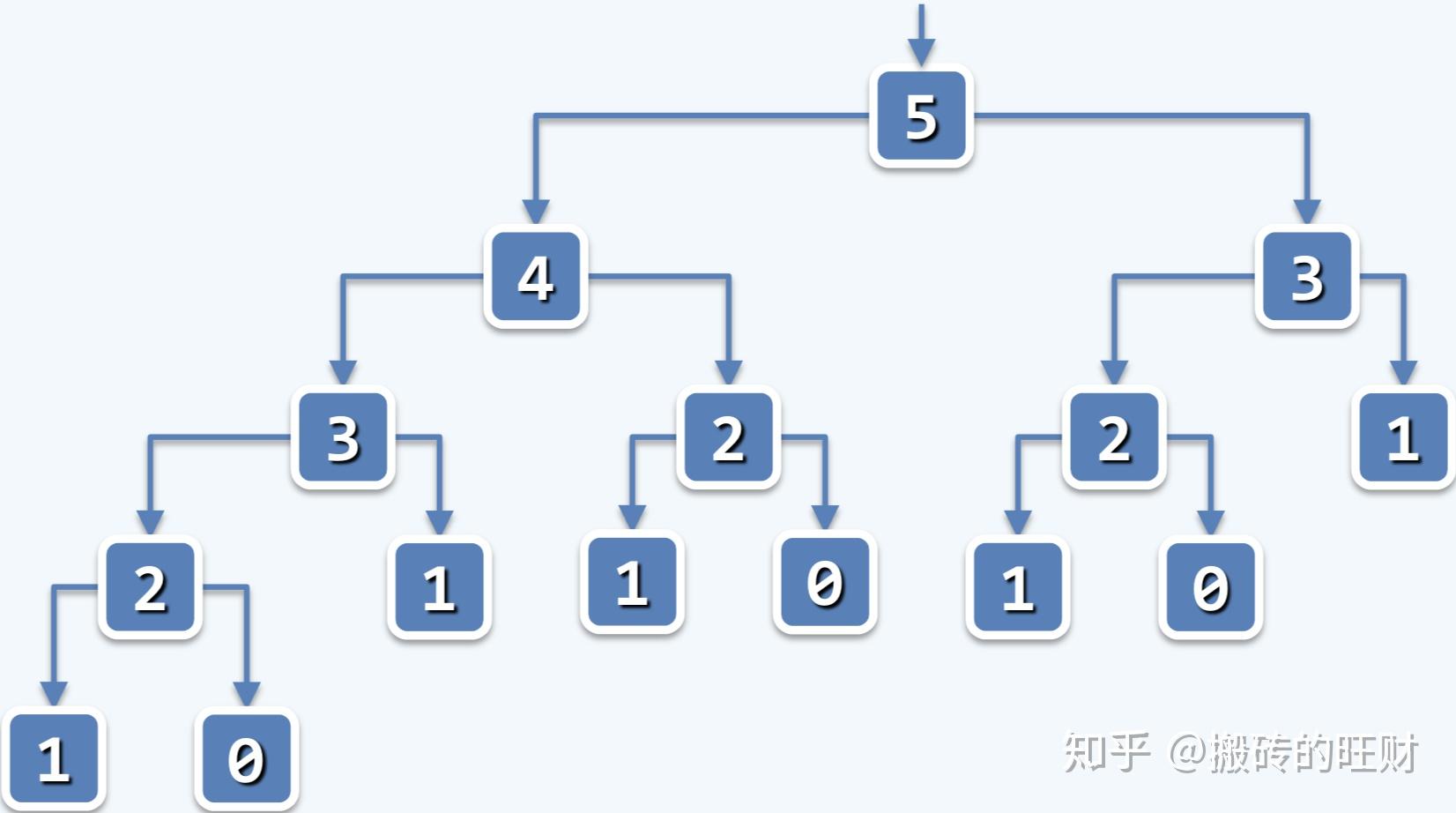
fib()：迭代解决方法A（记忆：memoization）：将已计算过实例的结果制表备查。
解决方法B（动态规划：dynamic programming）：颠倒计算方向，由自顶而下递归，为自底而上迭代。
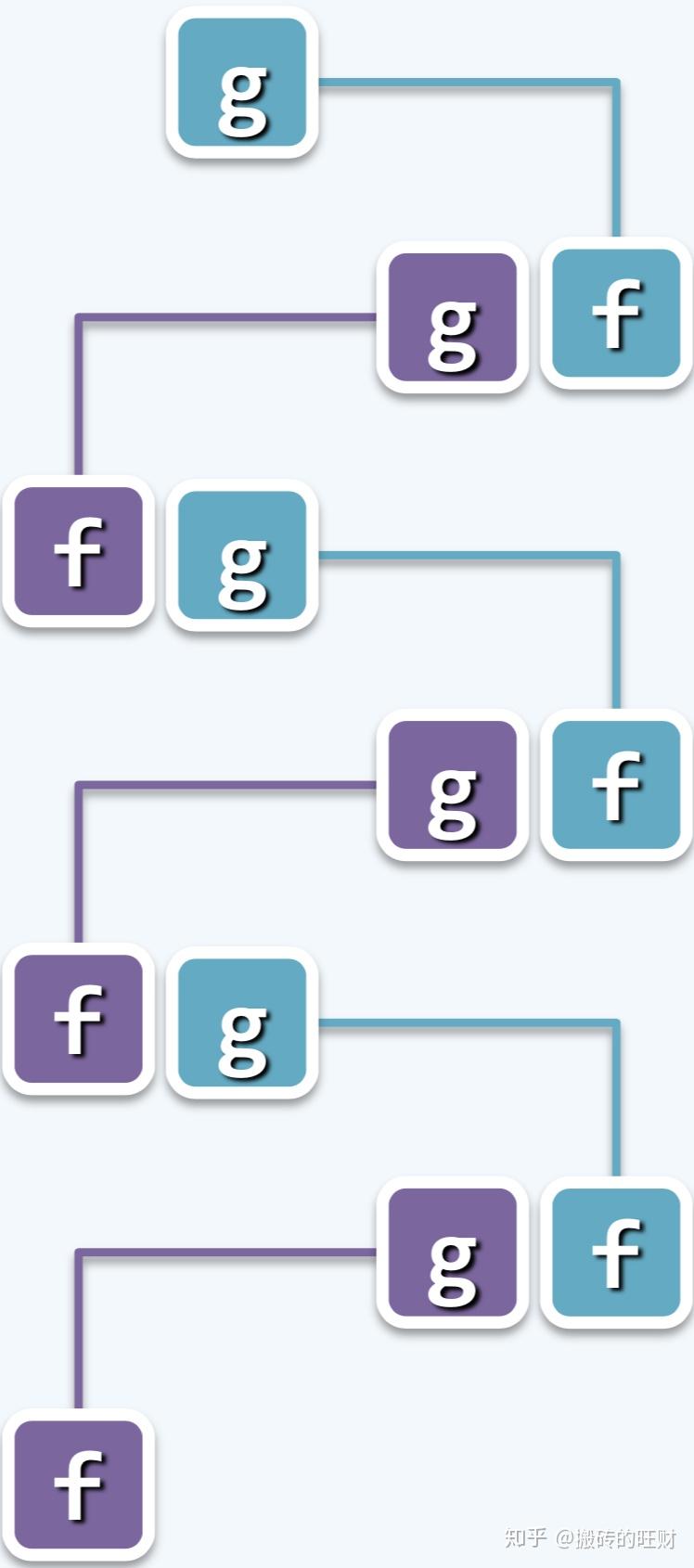滚动推进
多解
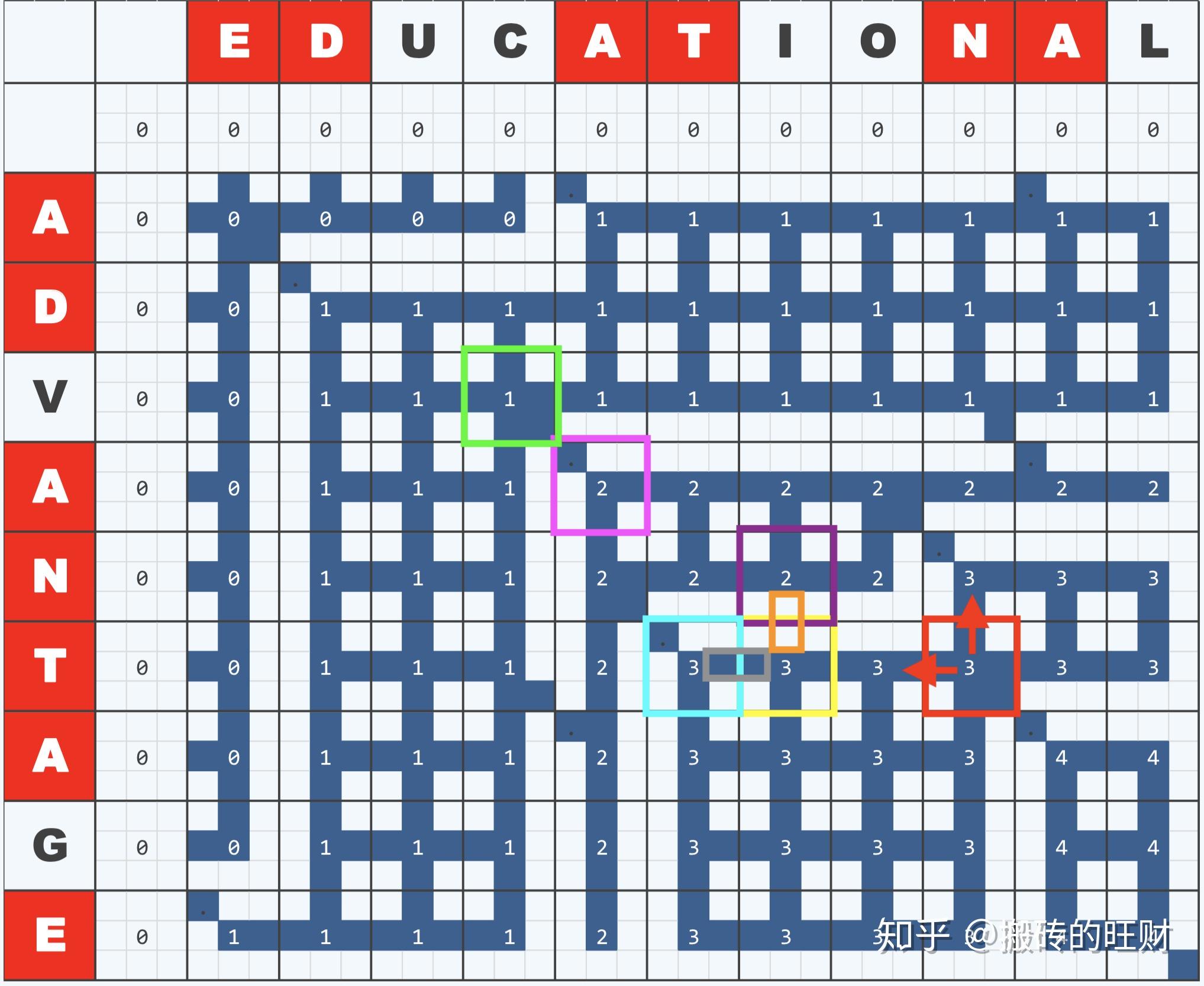
注释：第一大行和第一大列对应两个序列EDUCATIONAL和ADVANTAGE，每一大行和每一大列对应字符的九个小方格组成的大方格对应一个子任务，如果是减而治之的情况则绘制成对角线，例如图中粉红色的九宫格（对应EDUCA和ADVA序列子问题），此时把两个A抹除掉，继续去求解它左上角的子问题（绿色的九宫格，对应EDUC和ADV序列子问题，若结果为1，那么1+1=2为EDUCA和ADVA序列子问题的解），如果是分而治之的情况则需同时考虑左侧的子问题和上侧的子问题，例如黄色的九宫格（对应EDUCATI和ADVANT序列子问题），此时需同时考虑紫色的九宫格（对应EDUCATI和ADVAN序列子问题，结果为2）和蓝色的九宫格（对应EDUCAT和ADVANT序列子问题，结果为3），取结果较大者3，那么将通往较大者子问题的边保留下来（灰色的框），同时将通往较小者子问题的边抹掉（橘黄色的框）。当然，有的时候会出现歧义（图中红色的九宫格），此时的3可以理解为来自左边的子问题，也可以理解为来自上边的子问题。该图可以帮我们理解整个计算的过程，每一个LCS最终的解对应于从最左上角单元沿着可行的边（深蓝色）通往最右下角的单元的路径（多个解对应于多条可行的路径）。
歧义单调性：无论如何，没经过一次比对，原问题的规模必可减小。具体地，作为输入的两个序列，至少其一的长度缩短一个单位。
最好情况（不出现分而治之的情况）下，只需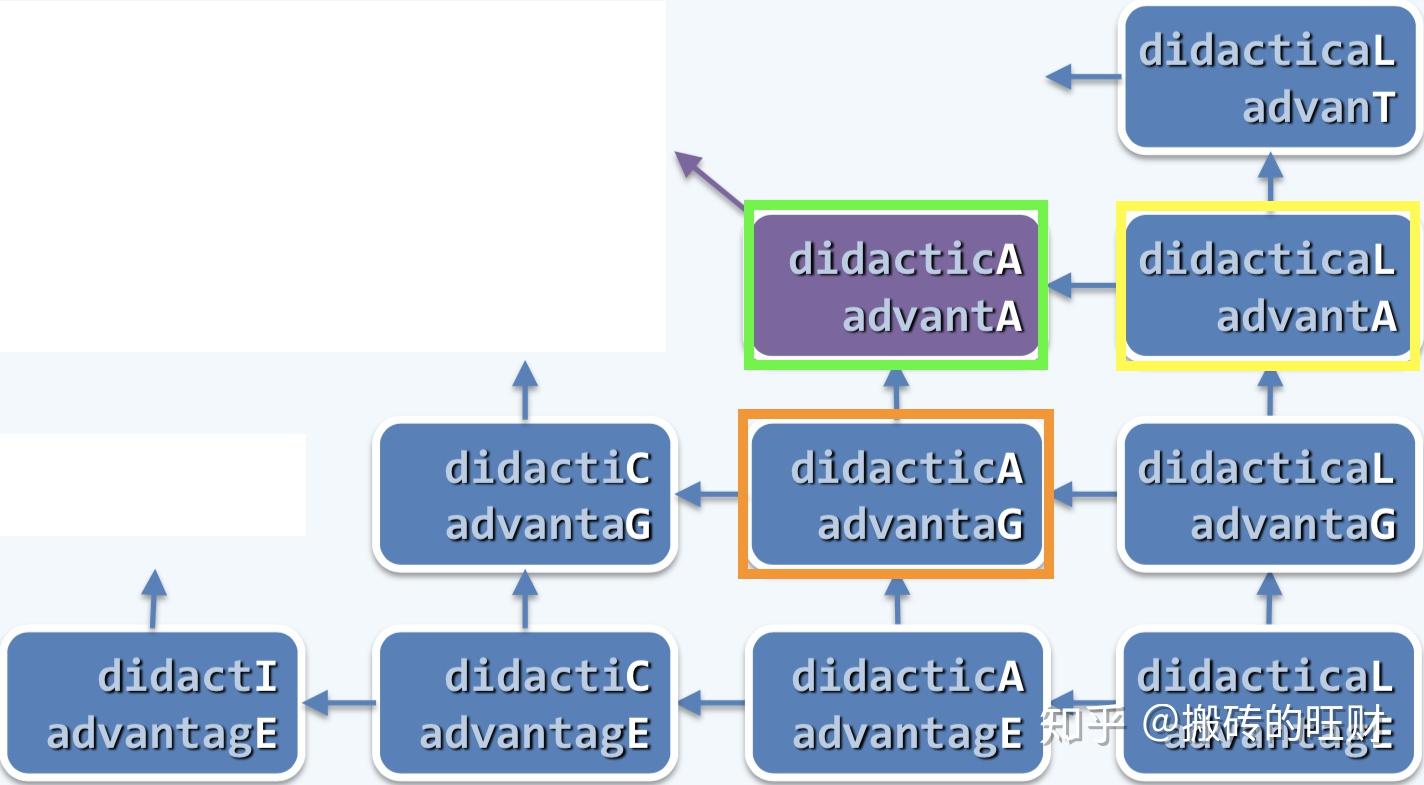 
橘黄色框对应的递归示例（didacticA和advantaG）和黄色框对应的递归示例（didacticaL和advantA）都将触发绿色框对应的递归示例，导致雷同。
为了求解出递归实例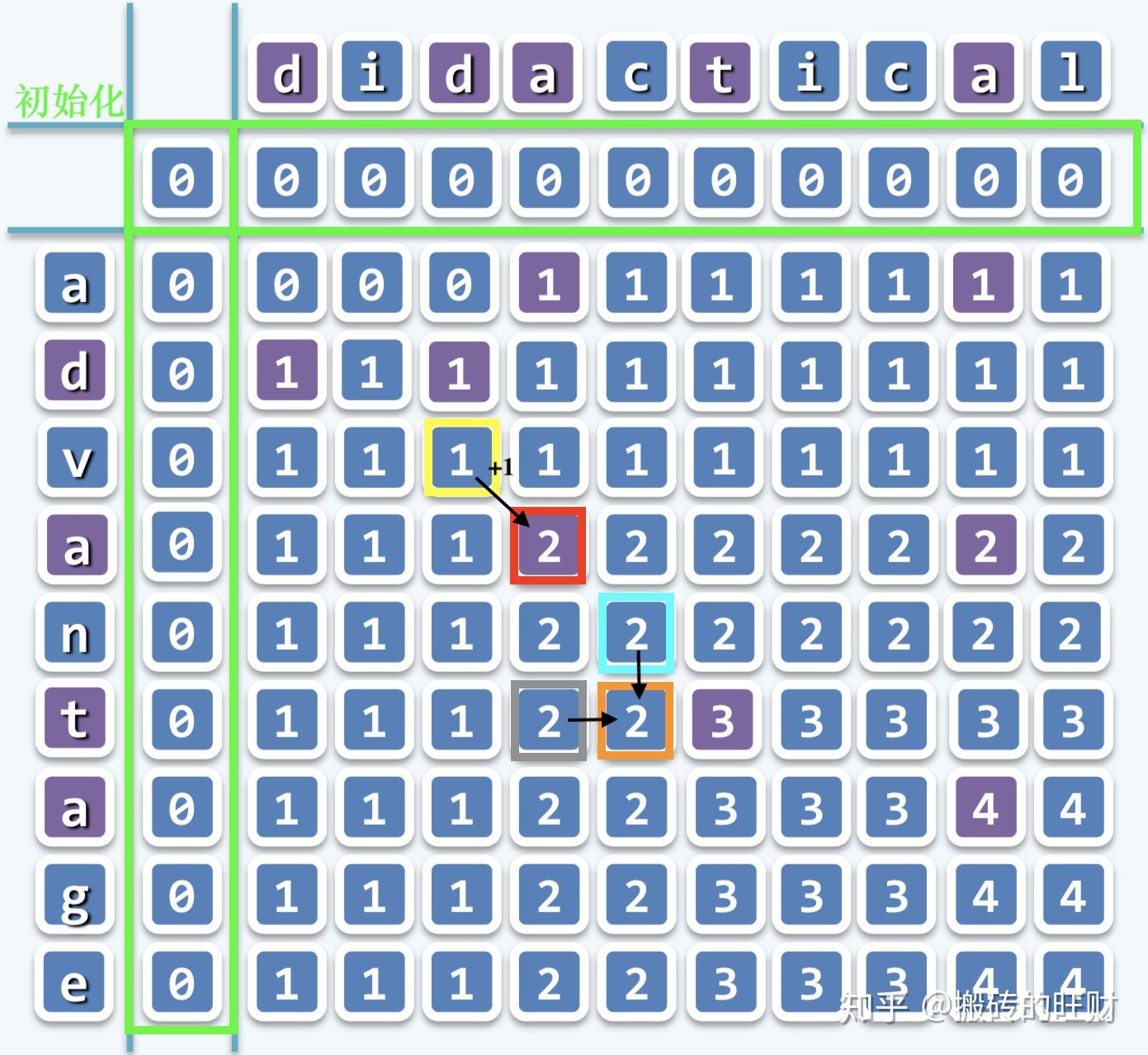 
请大家批评指正，谢谢 ～
（PS：以前写的东西还有很多的存货，有空我都会整理发到知乎，就当是再温习一下～）
